The classic puzzle

Game Structure

In the below picture of an old illustration of the game we see first the start position, a mid game position, and then the end position. This version of the game could be called a “3-8” game - 3 pegs, 8 disks.

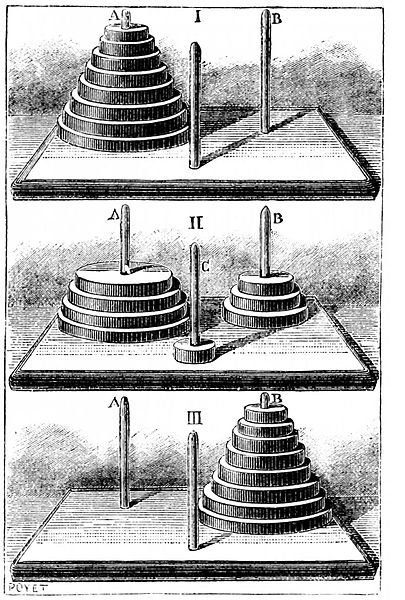
Aim and rules

The aim is to move the discs from the start peg to the destination peg (in this case the one on the right) using the spare peg in the middle. The following rules are to be adhered to:

1. Move only one disk at a time.
2. Move a single disk from the top of a tower and place it on another tower of empty peg
3. Disks must always sit on top of other larger disks or an empty peg

Mathematics of the game

We aim to complete the puzzle with as few moves as possible. For the 3 peg game, the minimum number of moves is:

min. moves = 2^n-1

Where n is the number of disks that we choose to play with. The power of the exponential means that a 5 disks game will require 31 moves, but a 10 disk game requires just over a thousand, and a 20 disk game over a million moves. It makes one wonder who has completed the largest version of this game, and how many disks!?

History of the puzzle

This puzzle dates from 1883 when it was published in Paris by a certain N Claus de Siam of the College of Li-Sou-Stian. The French involvement in IndoChina at that time expalins the names. In fact this name and college are anagrams of Lucas d’Amiens who was teaching at the Lycée Saint-Louis. The inventor of the puzzle was then the French mathematician Eduard Lucas who is best known for his results in number theory. In particuar he studied the Fibonacci sequence and the associated Lucas sequence named after him.

The “legend” which accompanied the game stated that in Benares in the reign of the Emperor Fo Hi there was a temple, with a dome which marked the centre of the world, beneath which priests moved golden discs between diamond needles, a cubit high and as thick as the body of a bee. The discs could be moved between needles, but only on the condition that no disc could be on top of a smaller one.

God placed 64 gold discs on one needle at the creation and it was the priests’ task to move all the discs to one of the other needles.

It was claimed that when they had completed the task, needles, tower, temple and Bramins would crumble away into dust and with a thunderclap the Universe would end.

Since it would have taken them at least 264−12^{64} - 1264−1 moves, which even at one move a second (and no mistakes!) would take over 580 billion years, that has never been tested. (source: https://mathshistory.st-andrews.ac.uk)

Read another more famous story of the power of the exponential

Research

interestingly contains a lot of hidden complexity. Finding proofs for optimal solutions for games with more than 3 Pegs turns out to be quite a challenge. The 4 Peg version as seen below is known as the Reve’s Puzzle:\

Many papers and essays have been written about searches for optimality within the games where p > 3 where p is the number of pegs in the game. The game graph of the p = 3 game is well known and mirrors the fractal known and the Sierpiński triangle. Having worked through what I think are optimal solutions for p = 4 and p = 5 games for values of n < 9 I believe that the graphs for games p > 3 also display a more complex (you might say higher-order) fractal nature.

[More to come here.]

---